Overview
In this project, I will implement a real-time simulation of cloth using a mass and spring based system. I will build the data structures to discretely represent the cloth, define and apply physical constraints on them, and apply numerical integration to simulate the way cloth moves over time. Finally, I will implement collisions with other objects as well as self-collisions to prevent cloth clipping.
This project is very interesting and it is simply astounding how we can make such realistic physical simulations based on very few, basic physics mechanisms. I cannot help but wonder what the physical simulations will look like if we incorporate more complicated and sophisticated physics into the simulation. I am definitely intrigued by this field of graphics and would like to explore in this domain.
Part 1: Masses and springs
Throughout the history of computer graphics, many different cloth models have been developed for simulation. Of these, one of the simplest models uses a system of point masses and springs, which I will use for this project.
Given a sheet of cloth with some desired dimensions and parameters, we can first divide the cloth up into evenly spaced point masses and then connect nearby masses with springs. If the cloth's orientation is horizontal, we set the y coordinate for all point masses to 1 while varying positions over the xz plane. Otherwise, we generate a small random offset between -1/1000 and 1/1000 for each point mass and use that as the z coordinate while varying positions over the xy plane.
Next, we add constraints between point masses via springs. There exists three types of constraints, which of all I've implemented in this project:
- Structural constraints exist between a point mass and the point mass to its left as well as the point mass above it.
- Shearing constraints exist between a point mass and the point mass to its diagonal upper left as well as the point mass to its diagonal upper right.
- Bending constraints exist between a point mass and the point mass two away to its left as well as the point mass two above it.
Below shows the detailed structure of my point masses and springs in a the cloth wireframe:
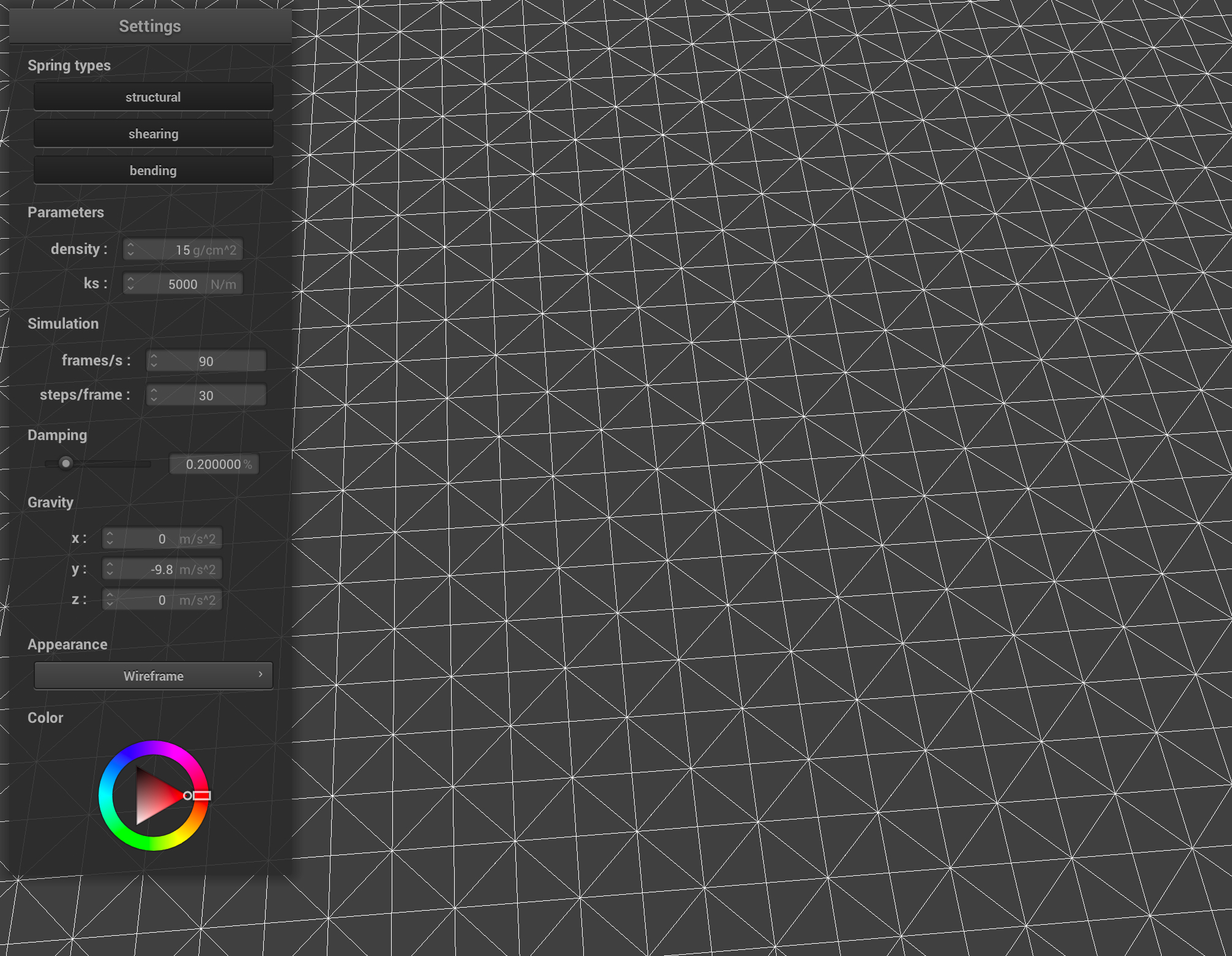
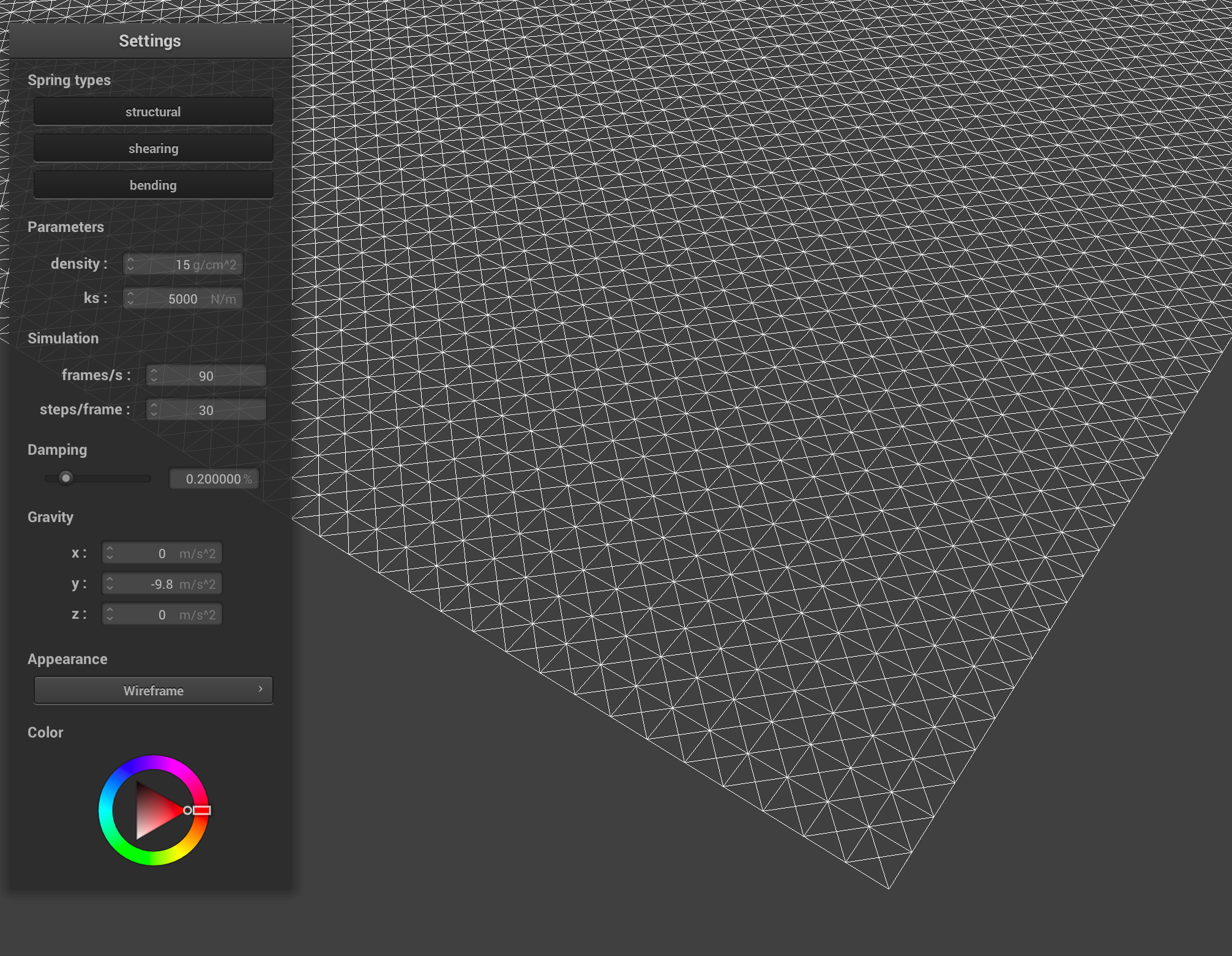
As we can see, point masses are evenly spaced out in the wireframe, with springs connecting each other forming a well defined structure.
Below shows what the wireframe looks like without any shearing constraints, with only shearing constraints, and with all constraints:




As you can see, shearing constraints are mainly the diagonal springs between point masses in the cloth wireframe to hold and maintain the square shape of cloth.
Part 2: Simulation via numerical integration
Now that we have set up the cloth model as a system of masses and springs, we need to integrate the physical equations of motion in order to apply the forces on our cloth's point masses to figure out how they move from one time step to the next.
Specifically, there are two kinds of forces: external forces such as gravity, which uniformly affect the cloth, and spring correction forces, which apply the spring constraints from before to keep the cloth together. The spring correction forces also vary between point masses based on the state of each spring.
To simulate this, we first uniformly apply the external forces on every point mass, and then compute the forces applied to the two masses on each spring using Hooke's law:
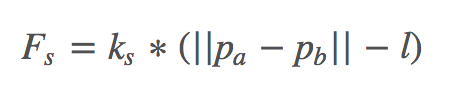
where k_s is the spring constant, p_a and p_b are the positions of the two masses, || indicates magnitude, and l is the spring's rest length. Because the bending constraint should be weaker that structural or shearing constraints, I use 0.2 * k_s as a weakened spring constant if the spring represents a bending constraint.
Having computed all the forces acted upon on each point mass for this time step, we perform numerical integration to compute each point mass's change in position. Here, I will use Verlet integration as follows
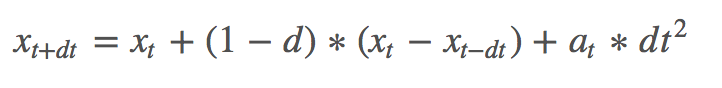
where x_t is the current position, x_t-dt is position from last time step, a_t is the current acceleration from all forces, d_t is the timestep, and d is the damping term that helps simulate the loss of energy due to friction, heat loss, etc.
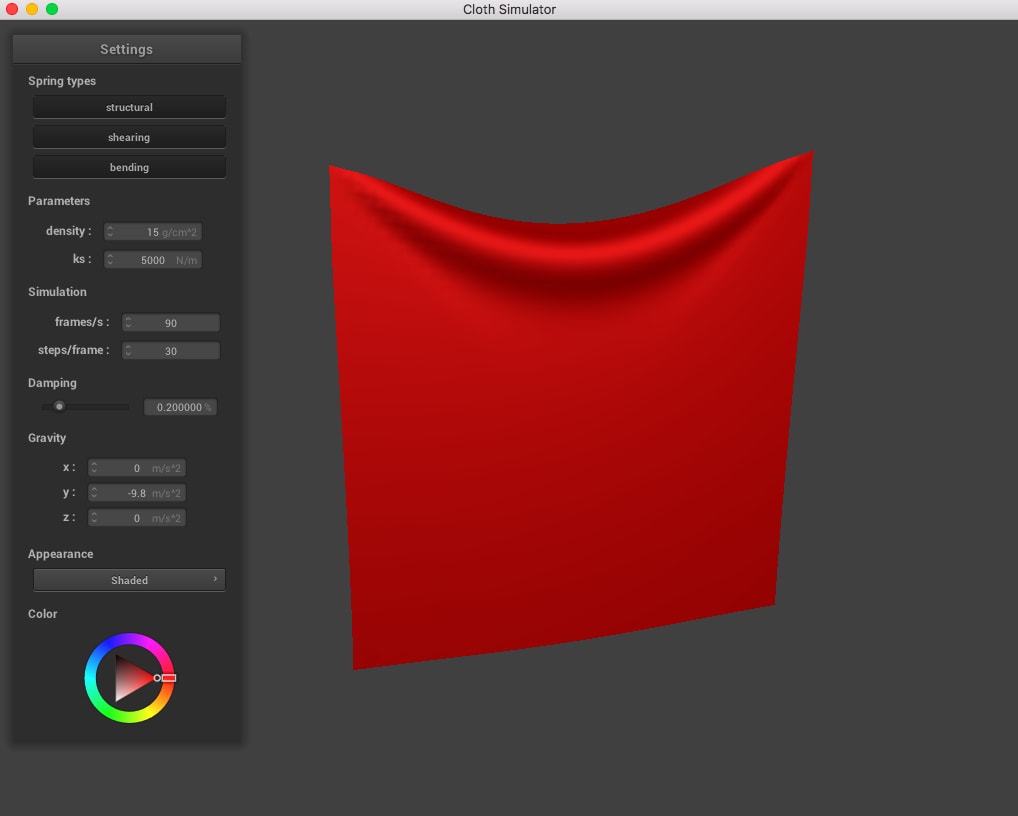
Here are some simulations for a falling cloth with two corners pinned:


The behavior and simulation of cloths also change as we modify the different parameters. Let's observe any noticeable differences in the cloth compared to the default parameters: spring constant k = 5000 N/m and density of 15 g/cm^2.
Below are side-by-side comparisons of the cloth with different spring constants.






As we can see, as we increase the spring constant, the cloth is less loose and the middle part of the cloth between the two pinned corners are less dragged down. It makes sense as a higher spring constant means a higher shearing constraint to prevent the cloth from changing the shape.
Below are side-by-side comparisons of the cloth with different density.






As we can see, as we increase the density, the cloth has more folds in the resting hanging state. It makes sense because a higher density means a larger mass given the total volume. A larger mass means a larger magnitude of external force applied to each point mass, given the same amount of external accelerations. It also means a smaller acceleration by the spring forces of shearing constraint, because the spring force magnitudes stay the same but the mass on which the spring forces applied has increased. Therefore, the total net effects causing more changes in the cloth appearance.
Below are side-by-side comparisons of the cloth with different damping.






As we can see, with a higher damping value, the changes in cloth appearance is relatively small. However, we indeed can still notice effects on the folds where a higher damping seems to produce folds that are more towards the side and the bottom and are less strong. This makes sense as a higher damping value introduces more loss of energy, causing the effects to be smaller.
Additionally, differences in damping also hugely impacts the animation of the falling cloths. For example, below shows two snapshots of the falling cloth, one with default damping d = 0.2, and one with low damping of d = 0.06. Specifically, we can find that cloths with low damping have more rippling when it falls, which makes sense as there's less loss of energy making the cloth look more bouncy and smooth.


Here is a simulation for a falling cloth with all four corners pinned:

Below are some views of a resting, shaded cloth with 4 corners pinned:




Part 3: Handling collisions with other objects
To make the sense look more interesting, I add support for cloth collision with other objects in the scene. Below I implemented collision support with spheres and planes.
To simulate collision with a sphere, we check if the point mass intersects with or is inside the sphere. If so, we "bump" it up to the surface of the sphere and let the point move towards, accounting for friction, the tangent point at where the point mass should have intersected the sphere, if it had traveled in a straight line from its position towards the sphere's origin.
Here are some simulations for a falling cloth onto a sphere:


Below are side-by-side comparisons of a resting cloth on the sphere with different spring constants.




As we can see, with a larger spring constant, the folds of the cloth when resting on the sphere tends to start from higher on the sphere surface and are more rigid to maintain its shape, letting edges of the cloth leaning more towards outside. In contrast, the cloth looks very smooth and soft and wraps around the ball more in a small spring constant case.
We can also simulate collisions with a plane. We do so by checking if a point mass moves from one side of the plane to the other in the last time step. If the point mass crosses over, we "bump" it back up to the side of the surface it originated from.
Here are some simulations for a falling cloth onto a plane:


Below is a picture of a not-so-interesting cloth finally resting on the plane:

Part 4: Handling self-collisions
The cloth should also be able to collide with itself as it falls onto itself and folds itself. We achieve this effect by implementing cloth self-collision: we apply a repulsive collision force if any pair of point masses on the cloth are too close to each other.
A naive method of implementing self collision is to loop through all pairs of point masses, compute the distance between them, and then apply a modifying force to the two point masses if they are within some threshold distance apart. However, this is O(N^2) time and is too inefficient for real-time simulations.
Instead, we accelerate it by using spatial hashing, where we divide the scene into equally sized 3D boxes and hash point masses to each of the boxes it resides in. Thus, we only need to compare the point masses within each 3D boxes. However, do note that it doesn't take care of the edge case when two point masses reside in different neighboring 3D boxes but also too close to each other because they are both very close to an edge. For the purpose of simplicity, I didn't take care of this case as it doesn't interfere with my simulation a lot.
Here are some simulations for a falling cloth onto a plane:


Below are screenshots of a falling cloth with default density (d = 15) and default spring constant (k = 5000). Take a look at how the cloth falls and folds on itself, starting with an early, initial self-collision and ending with the cloth at a more restful state.









Let's also observe how different parameters affect the behavior of the falling cloth.
Below shows a falling cloth with a density of 06:









Below shows a falling cloth with a density of 30:









As we can see, as we increase the density of the cloth, the cloth tends to have fewer subtle and small fold variations as it falls and folds itself. It also has larger and wider folds and tends to have more a bouncy look in a folded cloth for cloths with a large density.
Below shows a falling cloth with a spring constant of 500:









Below shows a falling cloth with a spring constant of 50000:









As we can see, the effects of changing spring constants are much more obvious than changing clot density. As we increase the spring constant of the cloth, the cloth clearly tends to have way fewer tiny and varied fold. The cloth with larger spring constant tends to have a consistent smooth and rigid look. It also folds more smoothly and constantly because the internal spring forces will keep the cloth more in shape as it falls. The cloth with larger spring constant also has wider folds in resting states.
